Towards a ‘Treatise’ of 7-Limit Harmony
Transformation and Prolongation in Extended Just Intonation
Extended Just Intonation: Background in Music Theory
In 1983, James Tenney introduced the term ‘harmonic space’ into post-tonal music. As pitches always signify more than just frequencies in a chromatic continuum, he concluded that, due to the harmonic relationships they involve, “the space of pitch perception is itself multidimensional.” 1 In view of more than a century of neo-Pythagorean research since Albert von Thimus’s Die harmonikale Symbolik des Altertums (1868), this statement emerged, however, rather as a revival of music’s premise as a “language of ratios” 2 under the influence of composing pioneers such as Harry Partch and Ben Johnston. The latter two had already laid the foundations for exploring microtonal relationships in just intonation: Partch 3 established his theory of harmonic limits in overtonal/superparticular and undertonal/subparticular tonality (subsequently abbreviated as O- and U-tonality); 4 Johnston 5 invented and put to use a reinterpretation of alteration symbols which he based on respective prime factors. 6
Harmonic limits set the margins of the arithmetic proportions to be involved by means of prime numbers. For example, traditional 5-limit thirds harmony can be imagined as the interaction of vectors in two spatial dimensions similar to a Cartesian coordinate system with two perpendicular axes. This method has been known since Leonhard Euler’s lattice 7 and was further developed by Hugo Riemann in his theory of harmonic dualism. 8 The scope of such representation on paper is quickly exhausted since pitches governed by higher prime limits require additional geometric dimensions. On the other hand, even 5-limit harmony exceeds the traditional concept of the twelve pitches once the intervals are tuned justly and without normalizing the commas that many harmonic sequences accumulate. Whatever the limit be, in order to achieve abundant diversity of harmonic transformations, intervals must be identified as ratios rather than mere stretches within a fixed pitch supply.
Even the polarity between O- and U-tonality can be expanded: As early as in 1930, Hans Kayser showed that the harmonic series could be unfurled in geometric interpolations of various complexity such as cubes and spheres. 9 For instance, his ‘tone-scale octagon’ uncovers a basic diatonic scale in limit 5 by projecting the harmonic series onto eight layers. In general, the overtone spectrum may be discarded as point of reference because the arithmetic nature of interval ratios alone allows for a sheer infinite variety of combinations. The only tools necessary are multiplication and division of fractions in contrast to the additive approach of the ‘smallest interval’ as it is known from serialism to set theory and many microtonal systems based on equal division. As Johnston observed correspondingly: “A great advantage which ratio scales have over all systems of temperament is that most of the latter are mutually exclusive, and the permutations of available intervals of each are finite and exhaustible, whereas all ratio scales are subsets of larger sets and are infinitely relatable and expandable.” 10
The perception of harmony does not rely on tradition and memory alone. However, in post-tonal music, the discourse on harmonic perception may still be impeded by persistent opinions from the post-war era, notably Theodor W. Adorno’s statements regarding tonality. 11 In contrast, discoveries in biophysics demonstrate that the auditory system processes musical intervals as periodic signals by synchronising pulsations in small integers from the potentially chaotic percept of acoustic information. 12 The simpler the ratio, the more consonant its impression, and even though neurons fire in the digital language of electric action-potentials, evidence shows that this hierarchical analysis is reflected in the topographic structure of the related brain stems. 13 Because pulsations in higher integers are filtered, the human ability to distinguish and reproduce music in extended harmonic limits may be physiologically restricted. This explains why harmonic limits are significant in the evaluation of consonance.
During the 20th century, various microtonal systems were notated by indicating a pitch’s difference from equal-semitone temperament. In some cases (such as Alois Hába’s stacked thirds 14 or Franz Richter Herf’s and Rolf Maedels’s 144-note scale for the International Society of Ekmelic Music 15 ) the creators sought to capture new territory in the harmonic spectrum – an attempt that was, in turn, compromised by the visible compulsion of temperament which their notation implied. Johnston’s limit-based alteration symbols, on the other hand, agreed with the scientific foundation of sound and the fact that by nature, the ear can be trained to intonate intervals justly. This premise was retained (as well as enhanced by erasing a few conflicts with conventional notation) in more recent approaches, led by a new generation of informed composer-theorists. While George D. Secor’s and David C. Keenan’s Sagittal Notation 16 could be thought of as something like a universal, phonetic transcription applicable to any conceivable interval size, Marc Sabat’s and Wolfgang von Schweinitz’s Extended Helmholtz-Ellis Just Intonation Microtonal Pitch Notation 17 (subsequently abbreviated as HE) was dedicated primarily to just intonation and, for its specific purpose, has retained a degree of simplicity comparable to an idiomatic alphabet. Both systems evolved around the same period, each relying on its own global network, numbering hundreds of composers and theorists, the former as Xenharmonic Alliance , the latter through the Plainsound Music Edition . My decision for HE in this study should be regarded as unimportant, since I will require only few accidentals in addition to common Pythagorean symbols.
My goal is to provide a simple trajectory to explore harmonic transformation in extended just intonation, stressing on a sense of “tonality” through which harmonic progressions can be verified by the ear. Due to the physiology of acoustic perception (as well as, to some extent, cultural conditioning) the effort of fine-tuning would remain useless or at least unrealised, as long as the composer’s decisions do not match a certain coherence dictated by rules very similar to tonal functions. As a common listener may understand 5-limit tonality even when it is performed using tempered or, to some degree, mistuned pitches, the general question arises whether the extension by one or two limits even requires just intonation under all circumstances. On the contrary, in some cases, temperaments may be preferable for more than practical reasons because by limiting the amount of possible transformations they create artificial pivot notes that can open hitherto unknown harmonic directions. A simple 24-note temperament, for instance, is able to approximate the harmonic three-quarter tone (11/12, 151 cents) almost exactly. By somehow magically planing limit 5’s syntonic comma, an 11-limit harmonic grid excluding prime factor 7 is achieved with an abundance of possibilities of its own. 18 That said, just intonation may be bypassed while still maintaining a rational understanding of harmonic relationships. By considering vertical (chordal) as well as horizontal (melodic) aspects, my investigation focuses rather on prolongation in the form of suspensions and different levels of dissonance to span larger structures.
In order to specify my results, I will restrict myself to a series of brief cadences in three voices, extending the traditional pitch supply of Western music by only a single limit (the seventh). Stepping up by one limit will introduce new harmonic vectors and thus more than just colour in the manner of a septième or onzième ajoutée .
Alteration Symbols in HE
HE disposes of a distinct set of accidentals for each prime factor up to (as of June 2020) 19 the 47th partial, although Table 1 displays just the first four of them. The three traditional Pythagorean accidentals – flat, natural, and sharp – are designed for a spiral of just fifths (3/2). Limit 5, based on the harmonic major third, is indicated by arrows attached to the traditional symbols, signifying an alteration by the syntonic comma (81/80). The limit 7 and 11 accidentals are added separately, signifying an alteration by the septimal comma (64/63) and one by the undecimal quartertone (33/32), respectively. In HE, it is customary to also provide cent values to indicate the difference to the common equal-tempered twelve pitches. Reference (=0) is standard chamber pitch, A natural.

Table 1 HE accidentals for prime factors 3, 5, 7, 11.Table 1: HE accidentals for prime factors 3, 5, 7, 11. 20
Exclusions
Tuning systems such as Harry Partch’s 11-limit 43-note scale 21 (displayed in fig. 1, using HE and a separate stave for each prime factor), may be mistaken for something like a ready-made palette so as to guarantee that “pure” intervals occur in all possible directions from any pitch to another. Nevertheless, certain rules must be observed to prevent the result from quickly deviating from a logical to an arbitrary succession. Apart from the general requirements of structural cohesion, many technically possible steps produce very complex fractions which one will find difficult to integrate in a harmonic sequence. The extent of ‘limit’ is not the issue here, but rather the way in which limits interact. For example, if I move from pitch 1 of the scale (fig. 1) to pitch 7 in the same row, (81/80) / (10/9) = (81/80) × (9/10) = (800/729), I will get a whole tone diminished by two syntonic commas in a very complex ratio, located in a remote octave of the harmonic spectrum and far away from each other. If, instead, I move from the same pitch 1 to pitch 6 in the 11-limit stave, (81/80) / (11/10) = (81/80) × (10/11) = (810/880) = (11/12), I get the harmonic three-quarter tone, an identical excerpt from the harmonic spectrum.

Figure 1 Lower half of Harry Partch’s 43-note scale in limit 11, written in HE.Figure 1: Lower half of Harry Partch’s 43-note scale in limit 11, written in HE.
Within Limit 11, Partch’s scale is designed to facilitate the more common transformations, preferably those in small integers. Comparable to the fixed pitch supply on some Middle-Eastern instruments (such as the qānūn ), it must be thought of as an inventory in which most adjacent notes never or only seldom appear next to each other. While its boundaries may be of lesser consequence in monophony, any progression involving more than one voice may have to be constructed carefully because all interval steps must obey the same rules.
The following examples (figs. 2–4) shall illustrate how smallest interval steps of Partch’s 11-limit scale may be integrated in harmonic transformation. The experiment is limited to a three-voice counterpoint, a constraint to help avoid conventional formulas such as the common triad. In figure 2, the upper voice moves chromatically from the fundamental pitch (G) to the diminished third of limit 7 (6/7). The numerals added to each note convert the pitches into partials of a harmonic spectrum. The interval ratios refer exclusively to the upper and to the bass voice, although the middle voice is equally restricted to justly tuned intervals. The main objective is to establish the harmonic quarter tone (32/33) as a chromatic scale degree. While the bass only requires limit 7, the second chord involves an inversion, very much like in conventional limit 5 tonal music. As one of several possible solutions, the example follows the premise that, if limit 5 is based on triads, limit 7 requires tetrads, limit 11 pentads, and so on – taken that, compared to the limit 5 tetrad (such as the dominant seventh), compared to the one of limit 7, constitutes nothing more than the system’s characteristic tendency to pile up thirds of different sizes. Accordingly, limit 11 chords may be thought of as pentads instead of triads, replenished by the harmonic seventh (4/7) and the harmonic fourth (8/11). This alone offers a multitude of different pitches to maintain harmonic tension, especially within the three-voice setup where pentads will never appear in their entirety.

Figure 2 Experimental chord progression by a diminished third (6/7) in the upper voice.Figure 2: Experimental chord progression by a diminished third (6/7) in the upper voice.
Audio Example 1 Experimental chord progression by a diminished third (6/7) in the upper voice.
The succession in figure 3 starts on an inversion and puts the harmonic quarter tone onto the first step, eventually reaching the harmonic minor third (5/6). The bass progression involves three adjacent levels in a theoretical spiral of harmonic sevenths. An interesting “false relation” occurs between the bass of the second and the middle voice of the third chord. Notably, the harmonic seventh as fundamental, compared to the harmonic fifth, behaves in inverse fashion: although the bass moves in U-tonal direction, the harmonic tension rises. The example concludes in a U-tonal chord, which is emphasised by reverse numerals. A variation of this model widens the first melodic step slightly by replacing the undecimal quarter tone with a septimal diminished semitone (fig. 4).

Figure 3 Experimental chord progression by a harmonic minor third (5/6) in the upper voice.Figure 3: Experimental chord progression by a harmonic minor third (5/6) in the upper voice.
Audio Example 2 Experimental chord progression by a harmonic minor third (5/6) in the upper voice.

Figure 4 Experimental chord progression to the harmonic minor second 5/6 in the upper voice, variation.Figure 4: Experimental chord progression to the harmonic minor second 5/6 in the upper voice, variation.
Audio Example 3 Experimental chord progression to the harmonic minor second 5/6 in the upper voice, variation.
Basic Transformations in Limit 7
In view of the overwhelming possibilities to combine smallest interval steps in extended just intonation, it may be good advice to explore limits by means of more systematic classification. First of all, certain boundaries must be established in order to categorise basic transformations. As a ‘skeleton’ of cadential resolutions, the following setup in 7-limit three-voice counterpoint will exclude intervals smaller than the harmonic major semitone (16/15). Ratios will be added to each voice movement.
The initial chord is O-tonal but may be thought of as containing some U-tonal quality, since the upper note, D4, will inevitably be regarded as a more common point of reference than the bass’s subharmonic seventh on which it stands. The harmonic seventh’s gravity affects the directions of voice leading. Model a sounds too sudden; a gap is perceived between the 7-limit three-note chord and the open fifths of its resolution. Model b closes this interruption but sounds too referential by simply resolving in the too-common major triad. This deficiency is overcome in model c by adding the diatonic major seventh (A sharp in the middle voice) (fig. 5).
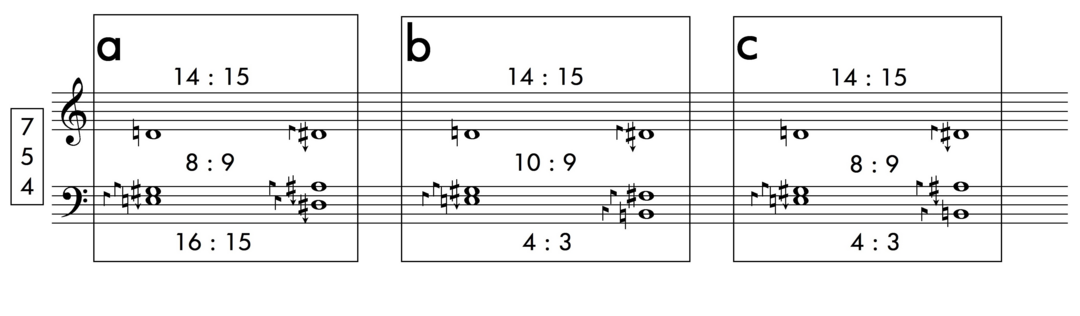
Figure 5 Basic resolution in limit 7.Figure 5: Basic resolution in limit 7.
Audio Example 4 Model a.
Audio Example 5 Model b.
Audio Example 6 Model c.
This observation hints at a general preference for seventh chords, involving both the harmonic minor and the major seventh while only the latter gives a feeling of resolution. In order to expand on this observation, the same cadence will now be modified (fig. 6). In model d, the first chord is transformed into its U-tonal relative. Consequently, the second voice starts from a lower pitch and can no more proceed to the A-natural of the second chord, respecting the ‘smallest interval rule’ established above.
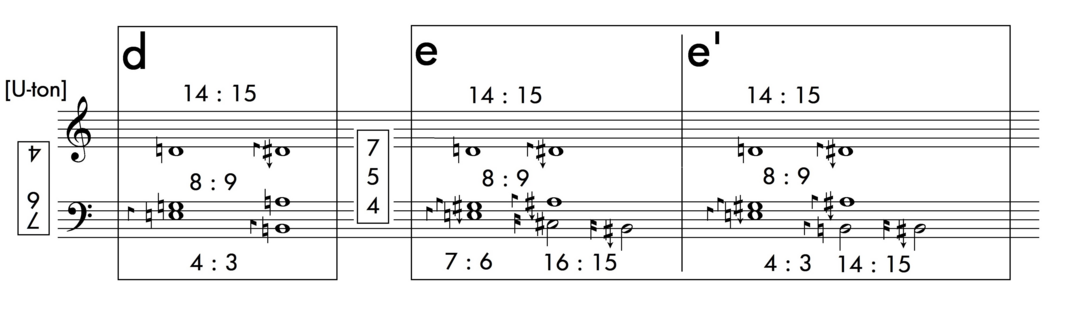
Figure 6 Simple modifications to the models a, b, c.Figure 6: Simple modifications to the models a, b, c.
Audio Example 7 Model d.
Audio Example 8 Model e.
Audio Example 9 Model e’.
Models e and e’ restore the first chord to its original O-tonal form but resolve into a remote U-tonal double-harmonic, half-diminished seventh. This is achieved by simply altering the bass note chromatically and using the diatonic major seventh (A sharp) as pivot (fig. 7). In this position, however, the chord emerges as an effective surprise. Because of its harmonic distance, it cannot be reached directly and thus requires a neighbouring note to tie the whole bass progression together in either diatonic (e) or chromatic (e’) steps.

Figure 7 U-tonal double-harmonic seventh, produced by chromatic alteration.Figure 7: U-tonal double-harmonic seventh, produced by chromatic alteration.
The following examples propose a different harmonic direction. While keeping the initial chord in its original O-tonal shape, the resolution of the upper voice introduces the harmonic major semitone and implies the same step as fundamental, although this note itself is omitted (fig. 8). Models f, f’, and g are related to the same chord in different distribution. Notably, in f’ a simple passing note provides additional micro-harmonic tension, the high D in the bass being fully embedded in a diatonic progression.

Figure 8 Alternative harmonic directions.Figure 8: Alternative harmonic directions.
Audio Example 10 Model f.
Audio Example 11 Model f’.
Audio Example 12 Model g.
In figure 9 the upper voice jumps within a range of practicable consonances, such as (6/7) in model h, and (5/6) in models j and k. One may elaborate on this pattern by including larger consonant intervals, such as the perfect fourth (3/4), the perfect fifth (2/3), and the minor sixth (5/8).
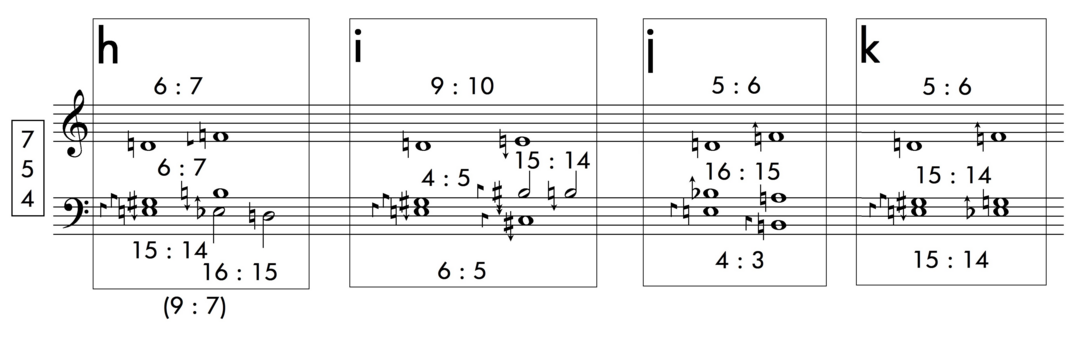
Figure 9 Further transformations.Figure 9: Further transformations.
Audio Example 13 Model h.
Audio Example 14 Model i.
Audio Example 15 Model j.
Audio Example 16 Model k.
Modulations Based on 5 and 7
One of the most obvious transformations in limit 7 involves the septimal subdiminished fifth (5/7), (7/5) and the super-augmented fourth (7/10), (10/7). Its attractivity (apart from being inconceivable in conventional limit 5 alone) stems from the fact that it combines two prime factors in inverse direction, moving in O-tonal direction in one and in U-tonal direction in the other, as the two-dimensional lattice of figure 10 illustrates.
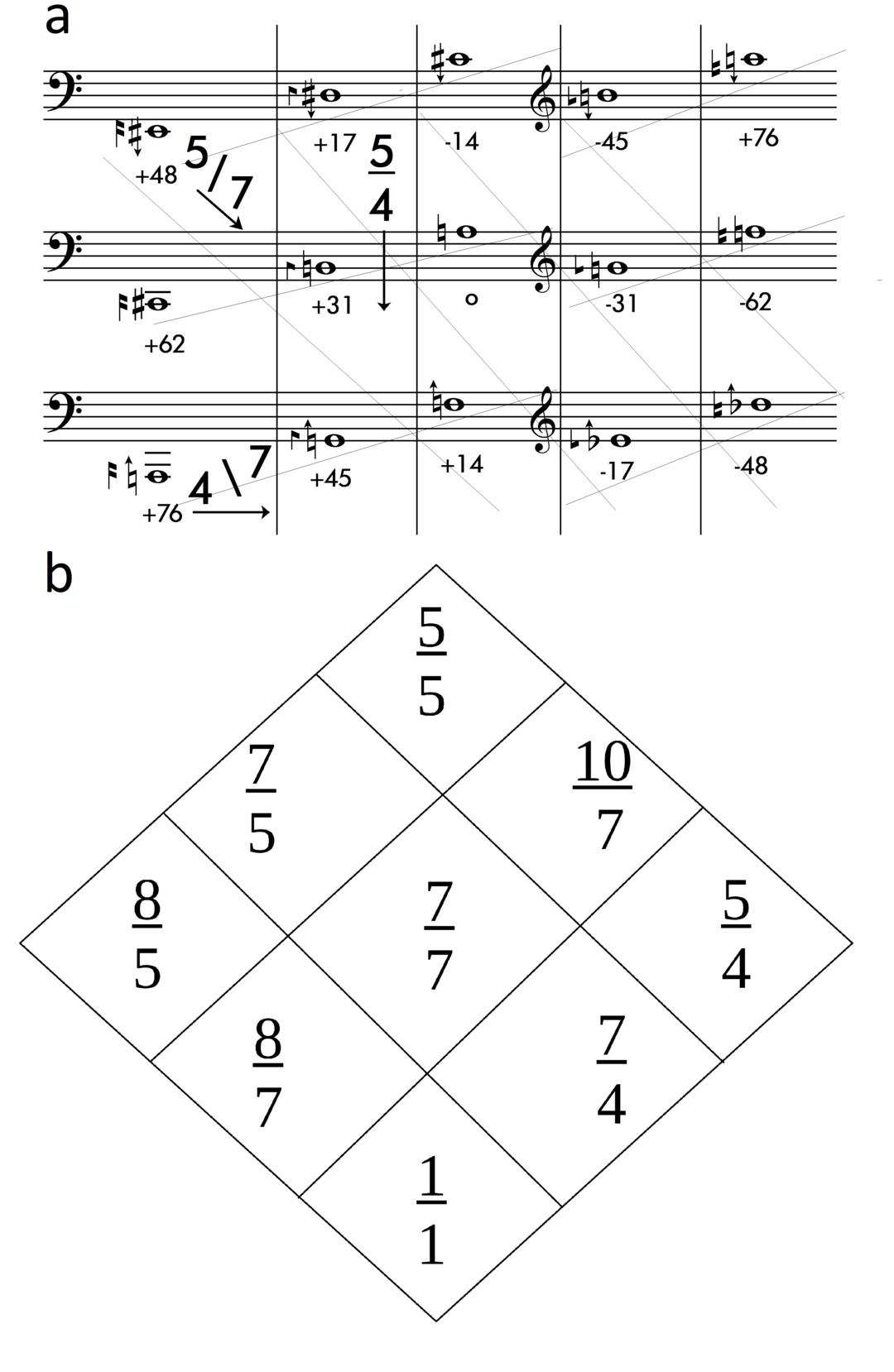
Figure 10 Transformations in prime factors 5 and 7 on a two-dimensional lattice (a), compared to a Partch-style tonality diamond (b).Figure 10: Transformations in prime factors 5 and 7 on a two-dimensional lattice (a), compared to a Partch-style tonality diamond (b).
Transformations resulting from the interaction between prime factors 5 and 7 are used extensively in my string quartet Rain from 2017. The focus lies on horizontal as much as on vertical aspects, creating a linear counterpoint of continuous suspension with temporary resolutions. Figure 12 shows a reduction of the stretta leading to the closing theme of the first section. 22 In imitative fashion, the upper voice and the bass progression unfold in similar interval sequences, although only the bass includes the perfect fifth and harmonic seventh. The appoggiaturas inserted in both lines serve more than ornamental purposes; they connect the surrounding pitches which otherwise could not be related by means of just ratios (example a). Note how the bass’s final step before the cadence (example b) is embedded in the structure by repeating the prior step of the upper voice (7/10) and reaching the double-subseventh on a U-tonal chord (fig. 12, bar 109) before closing the main cadence’s two-level resolution. Regarding the cadence, my reduction conflates its actual length for reasons of clarity.
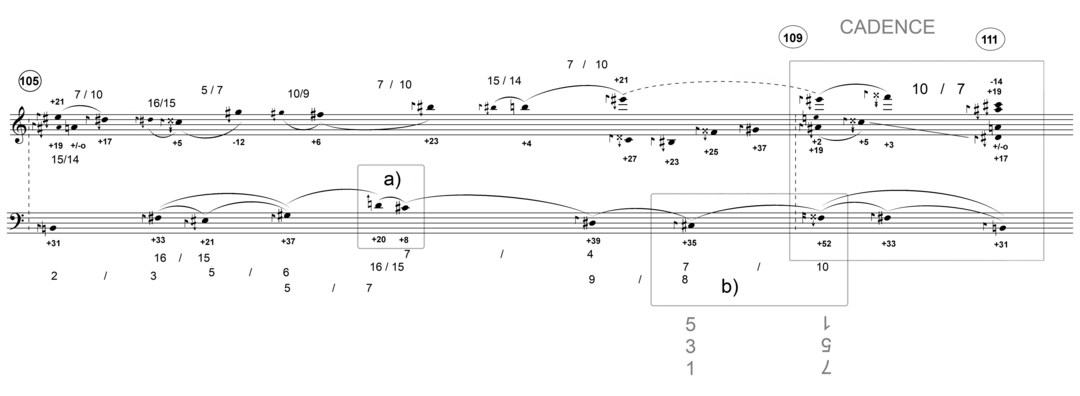
Figure 11 Stefan Pohlit, Figure 11: Stefan Pohlit, Rain : stretta leading into the closing theme of the first section in reduction.
The modulation to the Second Subject ( Seitensatz ) in Wolfgang von Schweinitz’s Plainsound-Sinfonie 23 from 2005 ends in similar fashion, connecting two distinct harmonic regions by the harmonic major semitone (14/15) – the septimal, slightly larger counterpart to the more common harmonic semitone (15/16). (In contrast to my approach outlined in the previous section, Schweinitz includes melodic steps smaller than (15/16) and (16/15), giving preference to vertical over horizontal consonance.) The lower double-stave in the reduction of fig. 12 summarises the events in the middle ground. The programmatic shift from the harmonic major third to the harmonic seventh (bar 25 in the score, fig. 11) can be taken as effective proof of the ‘multi-dimensional’ structure of extended just intonation. The difference between the pitches G flat + 26 cents (fig. 12, example a) and F sharp + 33 cents (fig. 12, example b) is no more than seven cents. How could it be of any noticeable significance without there being characteristic, rational identities at work?
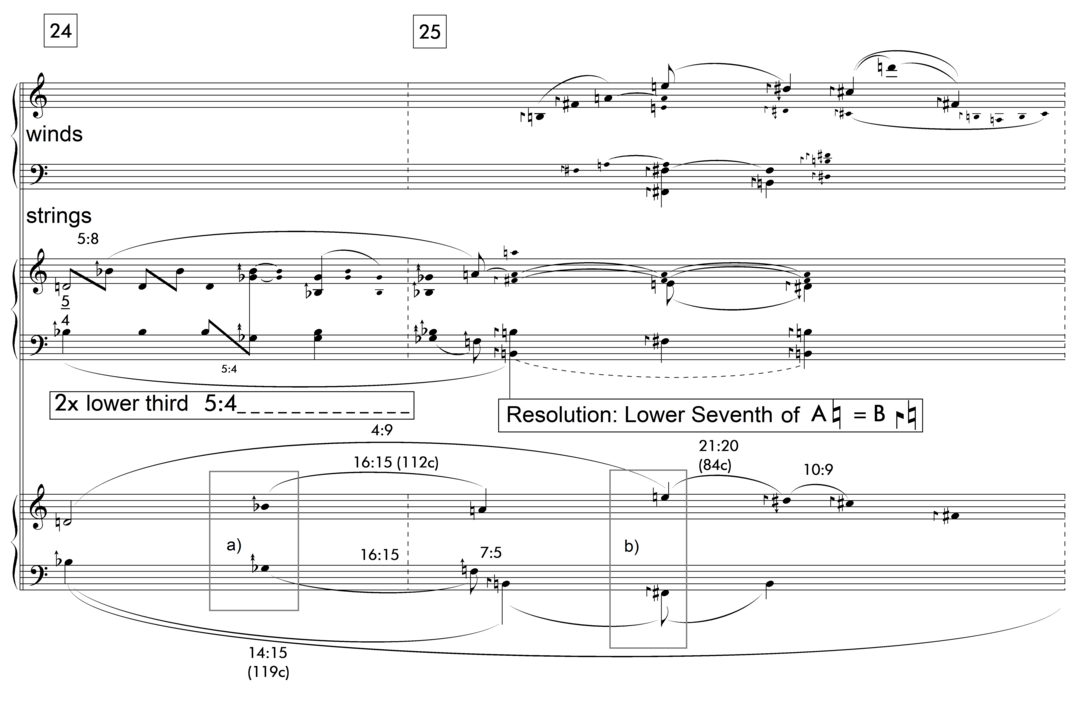
Figure 12 Combination of prime factors 5 and 7 in Wolfgang von Schweinitz’s Figure 12: Combination of prime factors 5 and 7 in Wolfgang von Schweinitz’s Plainsound-Sinfonie (Seitensatz: Die Naturseptime).
Quantity vs. Quality in Harmonic Music
In his dissertation, Daniel Huey distinguishes five levels of consonance/dissonance based on differential tones, from “triadic collection[s] of pitches belonging to the tuning area with the fundamental in the bass” to “collection[s] of pitches not belonging to [the] tuning area of [the] generating fundamental with conflicting pitches using the same letter name”. 24 In this sense, both the undecimal semi-augmented fourth (11/8) and the lesser tridecimal neutral sixth (13/8) figure among the consonant intervals of Huey’s second order: “7th, 9th, 11th, or 13th chord with all pitches belonging to tuning area with the fundamental pitch in the bass”. 25 Given that consonance is perceived in all possible harmonic structures alike (which would confirm just intonation as being something like a ‘universal language’ in harmonic music), this might be true. The thesis of this paper, however, is to substantiate whether a context instilled by specific prime limits may in fact overturn the weight of the most obvious consonances, such as harmonic fifths and thirds, in favour of more complex key intervals. As an example, let us consider Ivan Wyschnegradsky’s 24 Préludes for two pianos. In similar fashion as in J. S. Bach’s Well-Tempered Piano , the succession from one piece to another follows a cycle through all available keys – in this case 24, based on 24 pitches per octave and the undecimal semi-augmented fourth (11/8) as generator. As a principal building block of the composer’s 13-note gamut (“ chromatique diatonisé ”), (11/8) dominates resolutions to the tonic degree as early as in Prélude #2. 26 While one of the two pianos must be detuned by a tempered quarter tone (50 cents), the equal-semitone temperament on both instruments causes the semi-augmented fourth to sound in very close approximation to its harmonic ratio (550 cents instead of 551.32 cents) – closer even than the perfect fifth (700 cents instead of 701.96 cents). In response to Huey’s triadic argument, why should common listeners still perceive the available thirds and sixths as more consonant even though they are out of tune? Indeed, the more unconventional triadic chords in Wyschnegradsky’s Préludes (i.e. chords constructed by involving thirds and sixths with added or subtracted quarter tones, see Prélude #3, beginning) 27 sound out of tune rather than introducing a new, ‘tuneable’ harmonic quality.
This problem may be sufficiently explained by the physiological perception of harmonicity: According to Langner, the brain’s ability to differentiate and interpret musical intervals is inhibited by filter mechanisms that may reinterpret complex ratios as simpler ones (so called “spike intervals”). 28 Furthermore, “harmonic relationships may acquire the same perceptual quality simply by means of experience or learning.” 29 On the other hand, one may be able to distinguish interval sizes even without knowing how to identify and/or tune them by ear separately. Sabat and Schweinitz have provided a simple proposal to differentiate the definition of consonance in this sense: “[...] a consonance is an interval that may be exactly tuned by ear. This distinguishes consonances from tuneable dissonances, which may only be tuned by construction through a succession of consonances. Harmonic distance may then be considered to be a measure of the degree of consonance or dissonance of an interval, a property that Schönberg described as its comprehensibility.” 30 Regarding this “comprehensibility”, any full-fledged harmonic theory must allow the development of functions similar to 5-limit tonality, meaning that chords resolve in manners which audiences can anticipate.
Because “the number of new consonances decreases as the size of prime factors increases”, 31 an increase of limit adds a conspicuous case to this study: Similar to Hans Kayser’s “tone ratio” (the concept that musical intervals complement the arithmetics of vibration by expressing a sensual quality), harmonic perception involves both physiology and psychoacoustics. The argument that conventional thirds-harmony may convey psychological connotations seems as much trivial as it defies technological explanations provided through measuring and computation. However, without supposing that this phenomenon also exists and, in fact, may be developed in higher prime limits, the quest for harmonic complexity would appear (to me) only partially fulfilled. Beyond the scientific perfection of just tuning, I thus ask for the human being’s place in music as a link between ‘matter and psyche’. Kayser explored this qualitative dimension of music side by side with the quantity of interval sizes and ratios, looking at the “double aspect” 32 of Harmonics (consisting of arithmetical and sensual information) as something intrinsically alien to mathematics. As early as in 1965, Kayser’s successor Rudolf Haase opened an institute for harmonicist research (the “Hans-Kayser-Institut für Harmonikale Grundlagenforschung”) at the University of Vienna, developing topics of Kayser’s discoveries, such as “harmonic prototypes” 33 in the scope of academic inquiry. Taking into account this background, we may now understand the dilemma of complex triadic chord structures in Wyschnegradsky’s Préludes : Because our aural sense is trained to decipher thirds by means of harmonic and Pythagorean ratios (5/4, 81/64, and 6/5, 32/27), it misinterprets the new intervals as the old ones, recognising ‘false tuning’ rather than new harmonic qualities. We have thus entered a realm where computer-based inquiry must be replaced by practice and conscious immersion.
Conclusions
My investigations suggest that microtonal music can work in ways similar to conventional thirds-harmony (by means of transformations comparable to tonal functions), provided that its pitch organisation relies on a rational concept of intervals. Each prime factor unfolds in a distinct ‘dimension’, emerging as specific interval sizes and vectors in harmonic space. An effective harmonic network in higher limits operates on several levels, by dynamically linking, inverting and permutating different prime factors in O- and U-tonal directions.
A full explanation of these processes and their potential aesthetic or emotional qualities would require a systematic examination in form of a full-fledged functional theory of harmonic limits. This should include a labelling method to identify and compare transformations as well as strict hierarchies respecting natural degrees of consonance/dissonance besides a successive augmentation of limits. Rather than relying on algorithms and informatic approaches, I see no reason why this subject could not be addressed within the traditional scope of music theory, based on practice, ear analysis, and a conventional staff notation extended by the necessary alteration symbols. Beyond mere intellectual reasoning, the exploration must be developed incorporating a level of intuitive understanding and take into account the listener’s predisposition to comprehend harmonic structures as ‘meaningful’. Prime limits as a way to map harmonic complexity have not yet been sufficiently studied. This paper’s overall stance was thus to explore limit 7 first, before attempting harmonic structures in higher limits where the identification of consonance/dissonance degrees poses increasing difficulty.
References
- Adorno, Theodor W. (2006), Philosophy of New Music, ed. Robert Hullot-Kentor, Minneapolis: University of Minnesota Press.
- Euler, Leonhard (1739), Tentamen novae theoriae musicae ex certissimis harmoniae principiis, St. Petersburg: Academy of Sciences.
- Haase, Rudolf (1986), “Harmonikale Grundlagenforschung”, in: Acta Musicologica 58/2, 282–304. https://doi.org/10.2307/932817
- Helmholtz, Hermann (1954), On the Sensations of Tone, translated by Alexander J. Ellis, New York: Dover.
- Herf, Franz Richter (1986), “Komposition und Aufführungspraxis ekmelischer Musik”, in: Mikrotöne – Bericht über das internationale Symposium 10.–12. Mai 1985 in Salzburg, ed. by Franz Richter Herf, Innsbruck: Helbling, 224–36.
- Hesse, Horst-Peter (1996), “Alois Hába als Wegbereiter der mikrointervallischen und ekmelischen Musik”, in: Gedanken zu Alois Hába, ed. by Horst-Peter Hesse and Wolfgang Thies, Anif: Müller-Speiser, 45–56.
- Huey, Daniel (2017), Harmony, Voice Leading, and Microtonal Syntax in Ben Johnston’s String Quartet No. 5, Ph.D., University of Massachusetts Amherst. https://doi.org/10.7275/9470759.0
- Johnston, Ben (2006a), “A Notation System for Extended Just Intonation”, in: Maximum Clarity and Other Writings on Music, ed. by Bob Gilmore, Chicago: University of Illinois Press, 77–90.
- Johnston, Ben (2006b), “Rational Structure in Music”, in: Maximum Clarity and Other Writings on Music, ed. by Bob Gilmore, Chicago: University of Illinois Press, 62–76.
- Kayser, Hans (1993), Der hörende Mensch, Stuttgart: Engel.
- Langner, Gerald (1997), “Neural Processing of Periodicity Pitch”, in: Acta Oto-Laryngologica/Supplementum (Feb. 1997), 68–76.
- Partch, Harry (1974), Genesis of a Music [1949], New York: Da Capo Press.
- Pohlit, Stefan (2017), Rain, Berlin: Edition Juliane Klein.
- Riemann, Hugo (1873), Musikalische Logik: Hauptzüge der physiologischen und psychologischen Begründung unseres Musiksystems, Leipzig: C.F. Kahnt.
- Sabat, Marc (2005), The Extended Helmholtz-Ellis JI Pitch Notation, Berlin: Plainsound Music Edition. http://www.marcsabat.com/pdfs/notation.pdf (25.6.2020)
- Sabat, Marc (2020), The Helmholtz-Ellis JI Pitch Notation, revised by Marc Sabat and Thomas Nicholson, Berlin: Plainsounda Music Edition. http://marsbat.space/pdfs/HEJI2_legend+series.pdf (25.6.2020)
- Schweinitz, Wolfgang von (2005), Plainsound-Sinfonie – für Bassklarinette, Ensemble und Orchester op. 48, Berlin: Plainsound Music Edition.
- Secor, George D. / David. C. Keenan (2006), “Sagittal. A Microtonal Notation System”, in: Xenharmonikôn, An Informal Journal of Experimental Music 18. https://www.anaphoria.com/SecorSagittal.pdf (19.8.2023)
- Tenney, James (2015), “John Cage and the Theory of Harmony” [1983], in: From Scratch. Writings in Music Theory, ed. by Larry Polansky et al., Chicago: University of Illinois Press, 280–304.
- Wyschnegradsky, Ivan (1972), 24 Préludes en quarts de ton dans l’échelle chromatique diatonisée à 13 sons op. 22, Mainz: M. P. Belaieff.