Mathematische Remodellierung zur Erforschung der exakten Semantik einfacher konventioneller Notationssysteme
Was ist und wozu benötigt man die Spezifikation von musikalischer Notation? – Stand der Forschung
Die Regeln zum Lesen und Schreiben der konventionellen musikalischen Notation (Common Western Notation, CWN) wurden und werden hauptsächlich in der frühen musikalischen Ausbildung weitergegeben, in direktem Kontakt zwischen Lehrenden und Lernenden, im Kontext der praktischen Instrumentalausbildung. Ihre systematische Erforschung ist dafür offensichtlich nicht notwendig. Diese erfolgt davon unabhängig in ganz unterschiedlichen Kontexten und mit ganz unterschiedlichen Schwerpunkten. So begann in den 1960er Jahren im Kontext der ›Neuen Musik‹ der Darmstädter Sommerkurse eine intensive Diskussion über neuentwickelte, teils aus der CWN abgeleitete und in sie zu integrierende Notationsformen, die benötigt wurden, um neue Klang- und Spieltechniken, aber auch neue Arten von Synchronisierung, Freiheitsgraden und Zeitgestaltung darzustellen. Es ergaben sich eher technisch-pragmatisch ausgerichtete Beiträge wie eine über Jahrzehnte als Standard geltende Enzyklopädie, 1 die erst in jüngster Zeit einen Nachfolger fand, 2 und ein programmatischer Sammelband mit Beiträgen von Komponisten und Instrumentalisten. 3
Parallel dazu entstand aber, angestoßen nicht zuletzt durch die ›rein grafischen‹ Notate amerikanischer Komponisten, die eher grundsätzliche Debatte zur Ontologie des musikalischen Werkes, zu Sein- und Existenzformen des Kunstwerkes als solchem, in welcher die Frage nach dem Stellenwert von Notation eine zentrale Rolle spielt. Dies trifft sich mit der von der Philosophie her kommenden Behandlung derselben Frage, ausgehend von Ingarden über Goodman, Dahlhaus und Kurkela bis hin zu Nattiez. 4
Bemerkenswert ist, dass die CWN in fast allen Kontexten als Darstellungsmedium eingesetzt wird, ohne ihrerseits hinterfragt zu werden: Paläografologische Decodierungs-Ergebnisse werden zur Erklärung der Entzifferungsergebnisse in zeitgenössischer CWN dargestellt; 5 digitale Codierungen für Notation werden definiert, von MuseData 6 und Humdrum 7 bis MusicXML 8 und MEI; 9 Werke mit enzyklopädischem Anspruch beschäftigen sich mit allen möglichen Aspekten von grafischem Layout und Variantenbildung. 10 In all diesen Fällen aber wird die Bedeutung des CWN-Systems selbst als fraglos bekannt und wissenschaftlich unproblematisch vorausgesetzt: Wir entdecken/codieren/gravieren mit viel Aufwand eine Folge ›a-Viertel – g-Halbe‹, aber was das bedeuten soll, überlassen wir dem informellen Vorwissen der Leserin.
Die wenigen Fälle, in denen die Frage nach der Semantik des Aufgezeichneten tatsächlich gestellt wird, reichen von speziellen Untersuchungen zur Metrik 11 und zur Harmonik, ausgehend von der Problematisierung des syntonischen Kommas, 12 über verschiedene Tonhöhenmodelle 13 bis hin zu Reformvorschlägen für die Tonhöhennotation. 14
Es gibt u.W. nur eine einzige Monografie, welche die erkenntnistheoretische und mathematisch-konstruktive Frage nach der grundsätzlichen Weise der ›Hervorbringung von Bedeutung‹ durch das CWN-System explizit stellt. 15 Die momentanen Zentren der Notationsforschung sind, mit jeweils sehr unterschiedlichen Perspektiven: die Tenor-Konferenzen über digitale Erstellung, Transformation und Verbreitung von Notaten, die MEI-Konferenzen über digitale Encodierung und Annotation historischer Corpora, und das relative junge D-A-CH-Projekt Writing Music über Schreiben und Schriftlichkeit. In all diesen Kontexten finden sich immer wieder auch Beiträge zu der grundlegenden Frage nach der Semantik von musikalischer Notation. 16
Nicht zuletzt zeigt ja der 19. Jahreskongress der Gesellschaft für Musiktheorie, zu welchem vorliegender Text ein Beitrag ist, mit seinem breiten Spektrum unterschiedlichster Fragestellungen an musikalische Notation eindringlich die Vielfalt und Aktualität dieses Themas. Diese Aktualität ist nicht zuletzt politisch begründet: Die zunehmende digitaltechnische Automatisierung der Prozesse von Musikvermittlung, -speicherung, -weitergabe und -analyse droht mit der ›normativen Kraft des Faktischen‹ eine Überformung und Filtrierung der notationellen Traditionen vorzunehmen, wobei die Entscheidungen weniger Personen bei der Erstellung von Computerprogrammen, egal ob kommerziell oder public-domain, eine ganze Kulturtechnik zu determinieren drohen: »Such engraving programs [Sibelius, Finale] therefore may be said to represent a reactionary position to new music. Fortunately there are alternatives.« 17
Dem stellt unser Forschungsprojekt SemPart – Semantik der Partitur die Position entgegen, dass die tatsächliche Wirkungsweise der modernen CWN bisher nur in Ansätzen systematisch dargestellt und verstanden worden ist, und vor jede usurpierende Implementierung von Computersystemen die öffentliche Diskussion von Syntax und Semantik zu stellen sei.
Die angewandte Methode heißt ›Erforschung der Semantik von Musiknotation durch mathematische Remodellierung‹. Remodellierung bedeutet, dass jeweils ein kleines mathematisches Modell konstruiert wird, das einen bestimmten historisch-kulturell determinierten Dekodierungsvorgang ›nachbaut‹. 18 Dies geschieht für die verschiedenen Teilbereiche von Notation (Rhythmus, Tonhöhe, Lautstärke etc.) zunächst getrennt. Die angewandte mathematische Schreibweise erlaubt dann durch Modularisierung und Parametrisierung, verschiedene Teilmodelle zu kombinieren.
Das SemPart-Projekt basiert auf der Übertragung professioneller und sowohl praktisch bewährter als auch theoretisch fundierter Methoden aus der wissenschaftlichen Informatik, dort benutzt für den Entwurf und die Spezifikation von Computersprachen, auf das Zeichensystem der CWN. Bei diesen Verfahren werden zwei zunächst getrennte mathematische Modelle konstruiert: eines für die zu interpretierende Syntax und ein anderes für die möglichen Bedeutungen, und die ›Semantik‹ des Notationssystems wird aufgefasst als die beiden mathematischen Relationen, die zwischen diesen Sphären vermitteln.
Unsere ersten Schritte wenden dieses Verfahren auf eine basale Form der konventionellen Lautstärke-Notation mit expliziten Wertangaben (f, pp etc.) sowie Crescendo- und Diminuendo-Gabeln an. Bei dem Versuch, deren uns allen ›zur zweiten Natur‹ gewordenen Bedeutung in eine exakt definierte mathematische Semantik zu überführen, zeigten sich schon überraschend subtile Probleme und unvorhergesehene Komplikationen.
Als ein wichtiges Ergebnis kann die Erkenntnis gewonnen werden, dass es ›eine einzige zutreffende‹ Definition der Semantik, schon bei einem scheinbar so einfachen Symbolsystem, nicht geben kann, sondern dass nur ein Angebot an verschiedenen Definitionen adäquat ist, aus denen nach weitergehenden Analysen und Bestimmungen ausgewählt werden kann. Nicht selten muss sogar, um eine musikalisch sinnvolle Interpretation zu erzielen, innerhalb weniger Takte das Semantik-Modell vollständig ausgetauscht werden, so z.B. für eine Folge von Diminuendo-Gabeln im ersten Satz von Chopins b-Moll-Sonate. 19
Diese Erkenntnis bestätigt die Berechtigung der übergeordneten Strategie des Projektes, entnommen dem ›strukturtheoretischen‹ Ansatz in den Naturwissenschaften, bei dem ein mathematisches Modell zunächst ohne jeden inhaltlichen Anspruch auf Wahrheit oder Adäquatheit aufgebaut wird und erst a-posteriori die Fachwissenschaftler qua konkreter Anwendung der konstruierten Varianten über deren Aussagekraft entscheiden. 20 Das SemPart-Projekt macht nur Angebote zur Nomenklatur, wobei aber hinter jedem Begriff eine exakte, nachvollziehbare und algorithmische Definition steht. Was so gewonnen wird, ist ein Raster, das es ermöglicht, die aufgefundenen und notwendigen Varianten von Semantik eindeutig zu benennen, einzuordnen und zu vergleichen.
Techniken für die Definition von Computersprachen
Der große Bereich der Computersprachen umfasst alle speziell für die Mensch-Maschine-Interaktion entworfenen Sprachen, wie alle digitalen Programmier-, Konfigurations und Steuersprachen, lesbaren Datenrepräsentationen, HTML- und XML-basierten Textformate etc. Im Gegensatz zu natürlicher menschlicher Sprache wurden sie nur für einen bestimmten Zweck entworfen und haben deshalb eine einfachst mögliche syntaktische und semantische Struktur. 21 Darin ähneln sie stark der historisch herausgebildeten CWN, was durch die durchgehend erfolgreiche Anwendung ihrer klassischen Definitionsmethoden im Rahmen unseres Projektes nur bestätigt wird.
Abbildung 1 zeigt die grundlegenden Datenstrukturen und Informationsflüsse bei der Definition und Verarbeitung von Computersprachen. Eine erste und für das Thema der Analyse von musikalischer Notation entscheidend wichtige Festlegung ist, dass es zwei sauber getrennte Bereiche von mathematischen Objekten gibt, die man als ›syntaktische‹ und ›semantische‹ Sphäre bezeichnet. Erstere kommt mit relativ einfachen Konstruktionen aus: Computersprachen sind ja auf gute Verständlichkeit durch Mensch und Maschine hin entworfen worden und brauchen syntaktisch meist nur einfache Konstruktionen wie baumförmige Objektstrukturen o.ä. In der semantischen Sphäre hingegen darf die benötigte Mathematik für das Modellieren des Gemeinten so aufwendig werden wie nötig: Einheitenbehaftete Größen, intentional definierte Mengen, Automaten, Regel- und Inferenzsysteme etc. können je nach Bedarf hinzutreten.
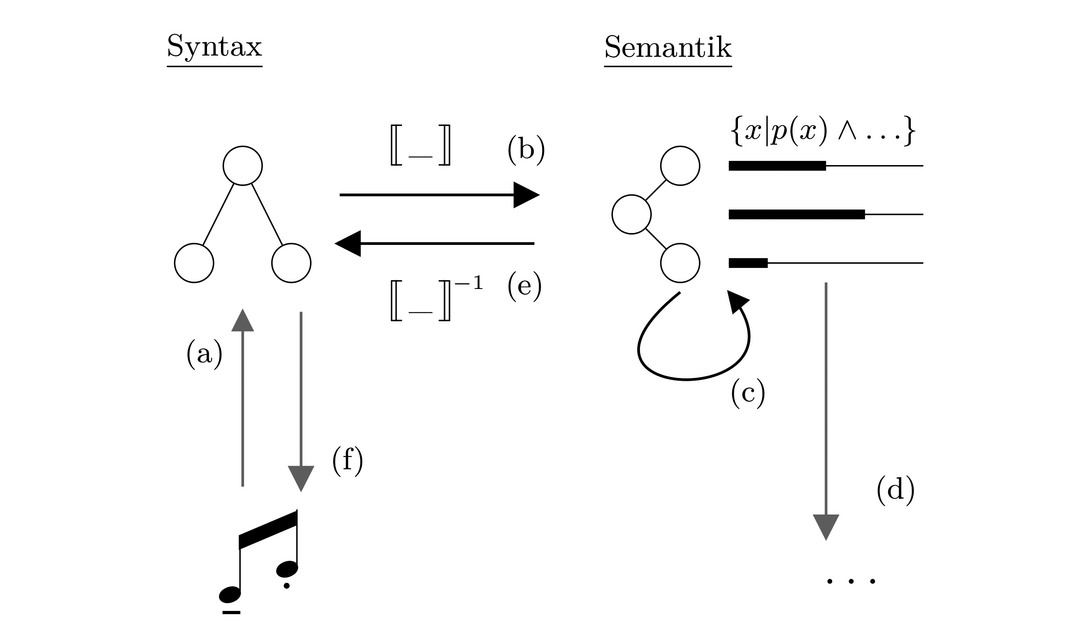
Abbildung 1 Übersetzungsvorgänge bei Computersprachen.
Man beachte, dass diese Definition der Sphären von ›Syntax und Semantik‹ eventuell nicht ganz deckungsgleich sind mit denjenigen der Linguistik, Semiotik etc. In ihrer Trennschärfe mögen sie ungewohnt erscheinen; sie sind eben ›Re-Konstruktionen‹ der Arbeitsweise des menschlichen Geistes, die selbstverständlicherweise nicht alle Phänomene von Unschärfe, Übergang, Mehrdeutigkeit und Unsicherheit der mentalen Praxis widerspiegeln. Dennoch meinen wir, dass sie als Prüfsteine der Nomenklaturbildung taugen und die Geisteswissenschaften hier von der Mathematik durchaus lernen können, im Sinne des computational thinking . 22
Bei unserer Analyse musikalischer Notation (hier: CWN) hat sich nämlich bald gezeigt, dass allein die scharfe Trennung dieser beiden Sphären schon weitreichend wohltuend zur Klarheit der Diskussion beiträgt. Aussagen über die syntaktische Gestalt und die gemeinte Semantik können sich sehr ähnlich sehen, sind aber etwas fundamental Verschiedenes. Dieser Unterschied kann in weniger streng strukturierten Diskussionen leicht übersehen werden und zu Missverständnissen führen.
Die Pfeile in Abbildung 1 stehen für die auf diesen Daten ausgeführten Transformations- und Übersetzungsprozesse:
a) Eine sogenannte ›externe Repräsentation‹ wird parsiert und in ein internes Datenobjekt (›Modell‹) der syntaktischen Sphäre übersetzt. Im Falle der üblichen Computersprachen ist die externe Repräsentation eine einfache Folge von menschenlesbaren Buchstaben, im Falle von CWN die Gesamtheit von Graphemen, bedeutungsvoll angeordnet in einer zweidimensionalen Ebene, auf einem Papier o.ä. Das interne Modell hingegen ist eine geordnete, vernetzte Ansammlung von mathematischen Datenobjekten.
b) Die interne Repräsentation der Syntax wird durch die Auswertungsfunktion ⟦ _ ⟧ in ein Datenobjekt der semantischen Sphäre übersetzt.
c) Dieses kann weiter modifiziert, ausgewertet, verändert, verfeinert werden, je nach Verwendungskontext. Darunter fallen z.B. die Auswertungsoperationen in logischen Programmiersprachen, die für den Benutzer nach einer oder mehreren ›Lösungen‹ suchen; im Falle musikalischer Daten hingegen Transpositionen, Tempomodifikationen, Filtrierungen, Analysen, etc.
d) Das interne Datenmodell kann in Effekte und Objekte der Realwelt übersetzt werden. Dies ist eine zentrale Anwendung, wenn das Gesamtsystem Steuerungsaufgaben in der Realwelt durchführen soll, wie Ansteuerung eines Synthesizers oder einer Lichtanlage.
e) Ein transformiertes Modell kann auch wieder zurückübersetzt werden in eine Syntax, und diese
f) kann weiter rückübersetzt werden in eine wieder menschenlesbare externe Repräsentation.
Anwendung dieser Techniken auf die Notation von Musik
Durch die Anwendung dieser Darstellungstechnik ergibt sich sofort eine harte Definitionsmöglichkeit für den Unterschied zwischen Semantik und Stil. Die Abbildung ⟦ _ ⟧, also Pfeil (b), ist eine Funktion im mathematischen Sinne: Jeder syntaktischen Gestalt darf nur ein einziger semantischer Gehalt entsprechen. Nicht aber umgekehrt, Pfeil (e). Hier sind mehrfache Umsetzungen durchaus üblich. Eigenschaften eines Notationssystems, die (b) beeinflussen, sind deshalb als ›semantische Unterschiede‹ zu bezeichnen, die nur (e) beeinflussen aber als ›rein stilistische‹. Diese wiederum können durchaus ›ergonomische‹ Konsequenzen haben, — alles drei sauber trennbare Begriffsfelder.
Dass (b) eine many-to-one oder one-to-one Relation ist, also eine echte ›Funktion‹ im mathematischen Sinne, ist unverzichtbar für dieses Verfahren. Darauf den Begriff der Semantik zu stützen erlaubt die gerade erwähnten harten Unterscheidungen und ist für unseren Ansatz zur Klärung der Begrifflichkeiten im Bereich der Musik zentral. Dies bedeutet aber keinesfalls, dass damit eine Eigenschaft der letztlichen musikalischen Interpretation bereits eindeutig entschieden wäre. Fast immer ist der Weg zum klingenden Resultat, wie weiter unten ausgeführt, ein längerer und er ist strukturiert als ein Netzwerk: 23 Im ersten Schritt (b) wird die externe Repräsentation meist auf einen noch rein symbolischen Wert abgebildet, dessen eigene ›Semantik‹ wiederum durch die Gestalt des nachgelagerten Verarbeitungsnetzwerkes (als Teil der Verarbeitungen (c), siehe die Abbildungen) erst definiert wird. Dadurch sind im weiteren Verlauf Auswahlen zwischen Bedeutungsvarianten, Modifikationen von Realisierungsverfahren, Freiheitsgraden, Interdependenzen zwischen musikalischen Parametern etc. durchaus möglich. Diese aber müssen allesamt exakt begründbar sein, also ableitbar aus anderen, parallel laufenden Parametern, die ihrerseits auf nämliche Weise dekodiert werden. Genau diese vernetzten Datenflüsse sind ja ein Hauptgegenstand z.B. des RUBATO-Projektes. 24
Rein technisch kann außerdem die geforderte eindeutige Abbildung (b) ja stets einen zusammengesetzten Typ als Zielbereich haben, so z.B. ein Produkt aus zwei Werten (wie ℚ×ℚ) als Minimal- und Maximalangabe eines Bereiches, oder der Potenzmengentyp (wie ℙℚ) für eine mögliche Auswahl an Werten. Fast immer aber sind die in den ersten Schritten der durch das Netzwerk definierten Semantikauswertung auftretenden Werte sowieso rein symbolisch, wie der unten beschriebene DDQ-Wert, und weitere Transformationen bis zum klingenden Ergebnis ohnehin erforderlich.
Die Arbeit im SemPart-Projekt beschränkt sich zur Zeit auf die Transformationen (b), (c) und (e). Unsere Untersuchung der metrum-konformen Rhythmus-Notation 25 folgt dem Weg (e), also wie ein gegebener Rhythmus durch eine Folge von Notenwerten repräsentiert wird, wenn die Spezifikation eines Metrums und ein Menge von Stil-Parametern gegeben sind. Die Untersuchungen zu Lautstärken und dem Auseinanderhalten von mehreren Stimmen, die sich ein Notensystem teilen, folgen hingegen dem Weg (b). 26 Alle diese Anwendungen stellten sich als überraschend kompliziert heraus – die Gewohnheit ihrer täglichen Benutzung überdeckte die nur sehr aufwendig zu modellierende Rand- und Extremfälle.
Gegenstand des Vortrages auf der Jahrestagung der GMTH in Zürich waren unsere Ergebnisse im Bereich der Lautstärke. Abbildung 2 zeigt in ihrem obersten Abschnitt eine Folge von einfachen Lautstärkewertangaben und Gabeln, bezogen auf die darüber symbolisch dargestellten ›Ereignisse‹.
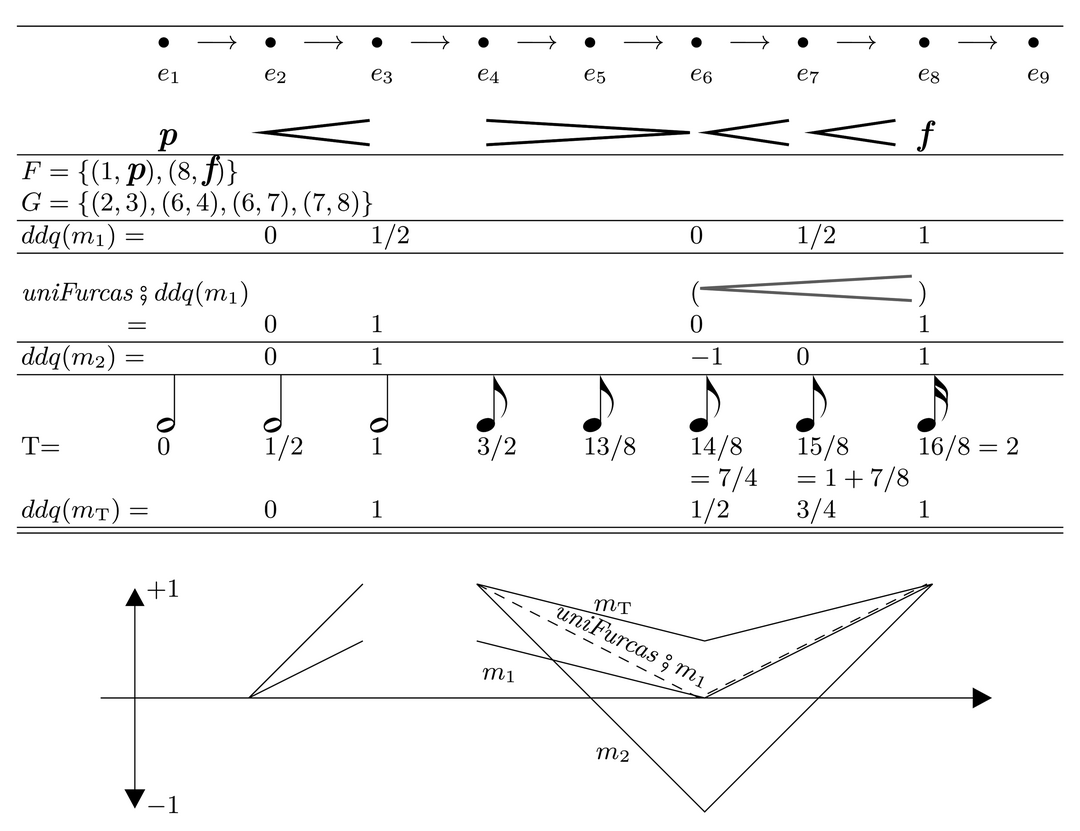
Abbildung 2 Einfache Lautstärkewerte- und Gabelfolge, die mathematische Codierung ihrer Syntax und die sich daraus ergebenden, verschieden parametrisierten DDQ-Semantisierungen.
Der nächste Abschnitt dieser Abbildung zeigt eine einfache mathematische Encodierung derselben Daten als Mengen F und G. Diese sind allesamt rein syntaktisch . Schon allein an diesen können die in Tabelle 1 aufgelisteten rein syntaktischen Eigenschaften abgelesen werden. Alle Eigenschaften von Notationssystemen und Notaten werden mit hierarchisch zusammengesetzten lateinischen Bezeichnern identifiziert; ihre inhaltliche Definition geschieht über konkrete, exakte und einfache mathematische Formeln, die hier nur die einfachen Eingangsdaten F und G verwenden. Sie sind formuliert in der Spezifikationssprache Z und werden in (parametrisierbare) Module zusammengefasst. 27 Das Erstellen dieser Module ist die eigentliche konstruktive Arbeit im Projekt. Durch die mathematische Modellierung werden die Eigenschaften von Notaten und Notationssystemen präzise, überprüfbar und unmissverständlich benennbar. Mag das für die obersten in der Tabelle noch überaus trivial anmuten, so sind die weiter untenstehenden deutlich anspruchsvoller zu berechnen und oftmals nicht sofort erkennbar.
|
nota.intensitas.sinIntens
|
|
nota.intensitas.sineFurca
Es gibt keine Gabeln.
|
|
nota.intensitas.iniDef
|
|
nota.intensitas.antiSymm
Es gibt zwischen zwei Ereignissen nur maximal eine Gabel.
|
|
nota.intensitas.singulFurca
|
|
nota.intensitas.furcae.beneTectae
|
|
nota.intensitas.singulModus
|
|
nota.intensitas.indexFurcarum.maximae (G)
|
|
nota.intensitas.indexFurcarum.maximae (G\nota.intensitas.indexFurcarum.maximae (G))
Menge aller Gabeln, die von genau einer anderen überspannt werden, etc.
|
|
nota.intensitas.indexFurcarum.indexFurcarum
Maximale Schachtelungstiefe aller vorhandenen Gabeln.
|
Tabelle 1 Die rein syntaktisch ablesbaren Eigenschaften von Notaten und Notationssystemen.
Obwohl hier noch überhaupt kein Begriff von Semantik vorliegt, wir uns also rein in der Oberflächlichkeit der Syntax bewegen, sind schon wichtige Kriterien definierbar, die Notate, Stile, Epochen, etc. unterscheidbar machen und digitale Werkzeuge (Software-Produkte oder Codierungsverfahren) exakt befragbar, wie z.B. »Bei Beethoven gilt immer nota.intensitas.singulModus bis auf eine einzige Stelle im Adagio der Pathétique« oder »in LilyPond gilt immer nota.intensitas.antiSymm «.
Die nächsten Abschnitte von Abbildung 2 zeigen jeweils Folgen von sogenannten DDQ-Werten als eine Möglichkeit einer semantischen Auswertung. Diese bestehen aus den die Gabelgruppe jeweils vorne und hinten umrahmenden Lautstärkewertangaben (genommen aus der Menge D, hier p und f) und einer Folge von rationalen Zahlen (aus der Menge ℚ), die für Interpolationswerte zwischen diesen beiden Polen stehen soll. Der letzte Abschnitt der Abbildung zeigt alle diese Folgen als Grafik.
Alle diese Folgen werden generiert von selben Algorithmus, der ebenfalls in einem Modul in der Sprache Z definiert ist und als Eingabe nur die Daten F und G erhält, die die Syntax repräsentieren.
Zusätzlich erhält der Algorithmus nur noch ein weiteres Funktionsargument (hier: m 1, m 2 , m T), das eine Maßfunktion auf die Länge jeder Gabel anwendet. Die verschiedenen Kurven entstehen durch die Auswahl unterschiedlicher Maßfunktionen. Je nach Beschaffenheit der syntaktischen Eingabe können mehrere oder gar (wie hier in der Abbildung) sämtliche möglichen Maßdefinitionen sinnvolle Semantisierungen liefern. Diese sind zunächst völlig gleichberechtigt; zwischen ihnen zu wählen bedarf weitergehender Bestimmungen und Regeln.
Die hier dargestellten syntaktischen Eingabedaten bilden einen einfachen Fall. Komplizierter sind Konflikte zwischen den Gabeln und den Rahmenlautstärken, die einen weiteren ›Kompensationsfaktor‹ als Parameter brauchen und damit unhintergehbar einen ganz neuen Freiheitsgrad in jede Interpretation einführen. 28
Für jede gegebene Gruppe von Gabelfolgen und DDQ Lautstärkewertangaben sind die Menge der anwendbaren Maße und die Menge der erlaubten Kompensationsfaktoren harte und algorithmisch bestimmbare semantische Größen.
Die Bedeutungen der Maßfunktionen sind:
m 1 = jede einzelne Gabel (als grafische Erscheinung) erhält denselben Lautstärkeunterschied.
m 2 = jedes einzelne überspannte Spielereignis (unabhängig von seiner Dauer) erhält denselben Lautstärkeunterschied.
m T = jede unter einer Gabel ablaufende Einheit der notierten Zeit erhält denselben Lautstärkeunterschied.
Ein typisches Ergebnis der mathematischen Remodellierung ist die Erkenntnis, dass nur in Verbindung mit Maßfunktion m 1 zwei aneinander anschließende, gleichgerichtete Gabeln eine andere Semantik (/Bedeutung/Auswirkung) haben als eine durchgehende, siehe den dritten und vierten Bereich in Abbildung 2. Im Rahmen unserer Remodellierung ist uniFurcas (..) eine Funktion, die solche Gabeln vereinigt, also die Menge G in die Menge { (2, 3), (6, 4), (6, 8) } überführt; die Modelleigenschaft selber (die auch im Kontext anderer Semantiken vorliegen oder fehlen kann) bekommt im Gesamtmodell den Namen nota.dyn.furcaSectaSignificans .
Wichtig ist, dass der sich ergebende DDQ-Interpolationswert noch völlig abstrakt und symbolisch ist. Bis am Schluss tatsächlich ein konkreter Amplitudenwert herauskommt (z.B. Beschleunigungsenergie einer Pianoforte-Taste oder Parameterwert ›a0‹ eines Synthesizeralgorithmus – letztlich die Energie des Schallfeldes im Raum), muss noch manch weiterer Transformationsschritt vollzogen werden. Abbildung 3 zeigt ein mögliches anschließendes Verarbeitungsnetzwerk (einschließlich alternativer Wege), in welchem ab und zu auch Parameter aus parallelen Notationsschichten gegenseitig verrechnet werden müssen. Dies entspricht dem Pfeil (c) in Abbildung 1.
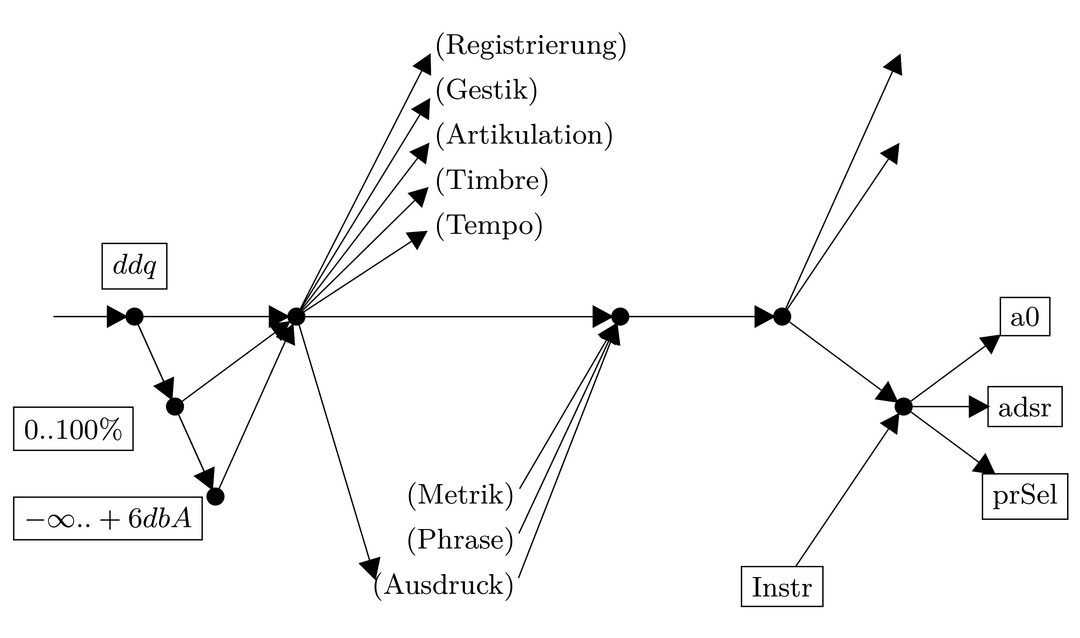
Abbildung 3 Mögliche Fortsetzungen der Verarbeitungspipeline.
Im Prinzip wird also die Semantik eines musikalischen Notationssystems durch ein solches Auswertungsnetzwerk definiert. Technisch und philosophisch entspricht dies dem Denken, das auch in einigen Rahmenwerken zur algorithmischen Komposition vertreten wird, wie OpenMusic , 29 oder zur algorithmischen Realisierung, wie das RUBATO-Projekt. 30 Es ist zu vermuten, dass sich Standardnetzwerke herausarbeiten lassen, dass es aber auch immer wieder Einzelwerke geben wird, die zur adäquaten Darstellung ihres Notates ein indviduell modifiziertes Netzwerk benötigen.
Derartige Remodellierungen stellen bloße Angebote zur Nomenklatur dar. Aus ihnen kann von den betrachtenden Wissenschaftlerinnen wie von den praktisch Ausführenden ausgewählt werden – sie können als zutreffend anerkannt oder verworfen werden. Unser Modellierungsprojekt will in keiner Weise Aussagen darüber treffen, wann und wo ein bestimmtes Semantik-Modell das richtige ist, sondern nur deren unhintergehbaren inneren Eigenschaften aufzeigen und damit die Konsequenzen, die man eingeht, wenn man sich für eines von ihnen entscheidet. An eine so berechnete Semantik können sich beliebige Transformationen anschließen, die beliebige Freiheitsgrade realisieren. Aber falls man behauptet, dass Notation eine Semantik habe, dann muss sie sich auf diese Weise darstellen lassen.
Der remodellierende, rein konstruktive Ansatz von SemPart erlaubt, dank den Möglichkeiten für ›Importe‹ und ›Parametrisierbarkeit‹ der zugrundeliegenden Programmiersprache Z, eine bruchlose Modellierung: Eine Verfeinerungskette wie ›CWN ganz allgemein‹ → ›Das Notationssystem der Wiener Klassik‹ → ›Alle Notate des mittleren Beethovens‹ → ›Das Notat der Fünften Sinfonie‹ → ›Das Modell der gestrigen Aufführung der Fünften Sinfonie‹ ist mit den nämlichen mathematischen Mitteln darstellbar. 31 Deswegen kann im obenstehenden Text immer austauschbar vom ›konkret gegebenen einzelnem Notat‹ oder vom ›in diesem Stil üblichen Notationssystem‹ oder von ›CWN im Allgemeinen‹ geredet werden: Die teils sehr strittigen Diskussionen über Stil, Stellenwert, Gültigkeit, Werkcharakter, Epochenabgrenzung etc. müssen für die Anwendung der konstruktiven Remodellierung nicht geklärt sein. Sie kommen logisch erst danach, sind von ihr völlig unabhängig. Sie können sich dann aber, das ist die Hoffnung, auf die Remodellierung gestützt einer präziseren Begrifflichkeit bedienen.
(Wir danken den anonymen Gutachtern für wertvolle Hinweise zur Verbesserung dieses Artikels.)
Literatur
-
Agostini, Andrea / Daniele Ghisi (2018), »Pitches in bach«, in:
Proceedings of the International Conference on Technologies for Music Notation and Representation – TENOR ’18
, hg. von Sandeep Bhagwati und Jean Bresson, Paris: Concordia University, 128–137. http://tenor-conference.org/proceedings/2018/17_Agostini_tenor18.pdf
(15.9.2023) - Aho, Alfred V. / Jeffrey D. Ullman (1977), Principles of Compiler Design, Reading: Addison-Wesley.
- Arlt, Wulf (Hg.) (1979), Paläographie der Musik nach den Plänen Leo Schrades, Köln: Arno Volk.
- Assmann, Jan (2020), »Schrift – Gedächtnis – Musik«, in: Musik und Schrift, hg. von Carolin Ratzinger, Nikolaus Urbanek und Sophie Zehetmayer, Paderborn: Wilhelm Fink, 51–66. https://doi.org/10.30965/9783846763537_003
- Bayer, Georg (1971), Einführung in das Programmieren in ALGOL . Berlin: Walter de Gruyter. https://doi.org/10.1515/9783111344218
- Broy, Manfred (2011), »Informatik als wissenschaftliche Methode: Zur Rolle der Informatik in Forschung und Anwendung«, in: 41. Jahrestagung der Gesellschaft für Informatik, Band P192 aus LNI, Berlin, 43–44.
- Celestini, Federico / Metteo Nanni / Simon Obert / Nikolaus Urbanek (2020), »Zu einer Theorie der musikalischen Schrift. Materiale, operative, ikonische und performative Aspekte musikalischer Notation«, in: Musik und Schrift, hg. von Carolin Ratzinger, Nikolaus Urbanek und Sophie Zehetmayer, Paderborn: Wilhelm Fink, 1–50. https://doi.org/10.30965/9783846763537_002
- Dahlhaus, Carl (1979), Musik als Text. In Dichtung und Musik. Kaleidoskop ihrer Beziehungen , Stuttgart: Klett-Cotta.
- Dimpker, Christian (2013), Extended Notation – The Depiction of the Unconventional, Wien: LIT Verlag.
- Fleischer, Anja / Guerino Mazzola / Thomas Noll (2000), »Computergestützte Musiktheorie. Zur Konzeption der Software RUBATO für musikalische Analyse und Performance«, in: Musiktheorie 15, 314–325.
- Goodman, Nelson (1976), Languages of Art. An Approach to a Theory of Symbols, Indianapolis: Hackett. https://doi.org/10.5040/9781350928541
- Gould, Elaine (2011), Behind Bars: The Definitive Guide to Music Notation, London: Faber.
- Hewlett, Walter B. (1987), »The Representation of Musical Data in Machine Readable Format«, in: Directory of Computer Assisted Research in Musicology , Vol. 3, Menlo Park: Center for Computer Assisted Research in the Humanities, 1–22.
- Hild, Elaine / Thomas Weber (2016), »Developing Encoding and Software Solutions. For the Digital and Analogue Publication of Medieval Monophonic Music«, in: Music Encoding Conference Proceedings 2013 and 2014 , hg. von Perry Roland und Johannes Kepper, 83–90. http://nbn-resolving.de/urn:nbn:de:bvb:12-babs2-0000007812 (15.9.2023)
- Huron, David (1995), The Humdrum Toolkit: Reference Manual , Menlo Park: Center for Computer Assisted Research in the Humanities.
- Ingarden, Roman (1962), Untersuchungen zur Ontologie der Kunst , Tübingen: Max Niemeyer. https://doi.org/10.1515/9783111717135
- Karkoschka, Erhard (1966), Das Schriftbild der Neuen Musik , Celle: Hermann Moeck.
- Klöckner, Stefan (2009), Handbuch Gregorianik. Einführung in Geschichte, Theorie und Praxis des gregorianischen Chorals , Regensburg: ConBrio.
- Kurkela, Kari (1986), Note and Tone: A Semantic Analysis of Conventional Music Notation , Helsinki: Coronet Books.
- Küppers, Bernd-Olaf (2000), »Die Strukturwissenschaften als Bindeglied zwischen Natur- und Geisteswissenschaften«, in: ders., Die Einheit der Wirklichkeit , München: Wilhelm Fink, 89–105.
- Lepper, Markus (2021), De Linguis Musicam Notare, Osnabrück: epOs. https://www.epos.uni-osnabrueck.de/buch.html?id=150 (15.9.2023)
- Lepper, Markus / Michael Oehler / Hartmuth Kinzler / Baltasar Trancón y Widemann (2019), »Diminuendo al bottom – clarifying the semantics of music notation by re-modeling, PLoS ONE 14(11): e0224688. https://doi.org/10.1371/journal.pone.0224688
- Lepper, Markus / Michael Oehler / Hartmuth Kinzler / Baltasar Trancón y Widemann (2020), »Crowded Staves – Rules for Semantics and Style of Conventional Multiple-Voices-Per-Staff Musical Notation«, in: Proceedings of the International Conference on Technologies for Music Notation and Representation – TENOR ’20, hg. von Rama Gottfried, Georg Hajdu, Jacob Sello, Alessandro Anatrini und John MacCallum, Hamburg: Hamburg University for Music and Theater, 1–12. http://tenor-conference.org/proceedings/2020/01_Lepper_tenor20.pdf (15.9.2023).
- Lepper, Markus / Baltasar Trancón y Widemann (2017), Metricsplit - Automated Notation of Rhythms, Adequate to a Metric Structure , Technical report, Technische Universität Ilmenau. http://markuslepper.eu/papers/msplit2016tr.pdf (15.9.2023).
- Lepper, Markus / Baltasar Trancón y Widemann (2019), »metricsplit: An automated notation of rhythm aligned with metric structure«, in: Journal of Mathematics and Music 13(1):60–84. https://doi.org/10.1080/17459737.2019.1600753
- Lerdahl, Fred / Ray Jackendoff (1983), A Generative Theory of Tonal Music, Cambridge: MIT Press.
- Maier, Michael (1998), »Vorschläge zur Reform der Notenschrift im 19. Jahrhundert«, in: Musik als Text. Bericht über den internationalen Kongress der Gesellschaft für Musikforschung Freiburg im Breisgau 1993 , hg. von Hermann Danuser und Tobias Plebuch, Kassel: Bärenreiter, 82–86.
- Malt, Mikhail / Benny Sluchin (2020), »Geometric Notation for Time-Bracket Works, Applications and Performance. The Case of John Cage’s Music for__«, in: Proceedings of the International Conference on Technologies for Music Notation and Representation – TENOR ’20, hg. von Rama Gottfried, Georg Hajdu, Jacob Sello, Alessandro Anatrini und John MacCallum, Hamburg: Hamburg University for Music and Theater, 114–119. http://tenor-conference.org/proceedings/2020/15_Malt_tenor20.pdf (15.9.2023).
- Mazzola, Guerino (1990), Geometrie der Töne: Elemente der mathematischen Musiktheorie. Basel: Birkhäuser. https://doi.org/10.1007/978-3-0348-7427-4
- Miller, Daniel (2017), »Are Scores Maps? A Cartographic Response to Goodman«, in: Proceedings of the International Conference on Technologies for Music Notation and Representation – TENOR ’17 , hg. von Helena Lopez Palma, Mike Solomon, Emiliana Tucci und Carmen Lage, Coruña: Universidade da Corunña, 57–67. http://tenor-conference.org/proceedings/2017/07_Miller_tenor2017.pdf (15.9.2023)
- Morris, Robert (2016), » Notation Is One Thing, Analysis Another, Musical Experience a Third: What Can They Have to Do With One Another?«, in: Music in Time: Phenomenology, Perception, Performance, hg. von Suzannah Clark und Alexander Rehding, Cambridge: Harvard University Press, 71–107.
- Nattiez, Jean-Jacques (1990), Music and Discourse. Toward a Semiology of Music , Princeton: Princeton University Press.
- Noll, Thomas / Monika Brand / Jörg Garbers / Andreas Nestke / Anja Volk (2004), Computer-Aided Representation, Analysis and Conveyance of Musical and Music-Theoretical Structures – Final Report, Berlin: Technische Universität Berlin. www.tu-berlin.de/fileadmin/fg53/KIT-Reports/r149.pdf (22.9.2020, use wayback machine)
- Nuño, Luis (2020), »Representation of Harmonies on the Harmonic Wheel«, in: Proceedings of the International Conference on Technologies for Music Notation and Representation – TENOR ’20, hg. von Rama Gottfried, Georg Hajdu, Jacob Sello, Alessandro Anatrini und John MacCallum, Hamburg: Hamburg University for Music and Theater, 24–32. http://tenor-conference.org/proceedings/2020/03_Nuno_tenor20.pdf (15.9.2023).
- Oettingen, Arthur von (1913), Das duale Harmoniesystem, Leipzig: Siegel.
- Plaksin, Anna (2020), »Do Visual Features Matter? Studies in Phylogenetic Analysis of Mensural Music«, in: Music Encoding Conference Proceedings , hg. von Elsa De Luca und Julia Flanders, Humanities Common, 87–94. http://dx.doi.org/10.17613/mvxw-x477
- Fournier-S’niehotta, Raphaël / Philippe Rigaux / Nicolas Travers (2016), »Is There a Data Model in Music Notation?«, in: Proceedings of the International Conference on Technologies for Music Notation and Representation – TENOR ’16, hg. von Richard Hoadley, Chris Nash und Dominique Fober, Cambridge: Anglia Ruskin University, 85–91. http://tenor-conference.org/proceedings/2016/12_Fournier_tenor2016.pdf (15.9.2023).
- Read, Gardner (1979), Music Notation. A Manual of Modern Practice , New York: Taplinger.
- Riemann, Hugo (1878), Studien zur Geschichte der Notenschrift , Leipzig: Breitkopf & Härtel.
- Ross, Ted (1987), The Art of Music Engraving and Processing , New York: Hansen Books.
- Sabbe, Herman / Kurt Stone (Hg.) (1975), International Conference on New Musical Notations: Report. Ghent: State University.
- Schmid, Manfred Hermann (1998), »Schrift der Moderne und Musik der Vergangenheit«, in: Musik als Text. Bericht über den internationalen Kongress der Gesellschaft für Musikforschung Freiburg im Breisgau 1993 , hg. von Hermann Danuser und Tobias Plebuch, Kassel: Bärenreiter, 78–81.
- Schmidt, Dörte (2020), »Schrift. Werk. Performance. Neue Musik«, in: Musik und Schrift, hg. von Carolin Ratzinger, Nikolaus Urbanek und Sophie Zehetmayer, Paderborn: Wilhelm Fink, 275–300. https://doi.org/10.30965/9783846763537_011
- Sköld, Mattias (2018), »Combining sound- and pitch-based notation for teaching and composition«, in: Proceedings of the International Conference on Technologies for Music Notation and Representation – TENOR ’18 , hg. von Sandeep Bhagwati und Jean Bresson, Paris: Concordia University, 1–6. http://tenor-conference.org/proceedings/2018/01_Skold_tenor18.pdf (15.9.2023)
- Spivey, J. M. (1988), The Z Notation. A Reference Manual , Prentice Hall: International Series in Computer Science.
- Stone, Kurt (1980), Notation in the Twentieth Century. A Practical Guidebook , New York: Norton.
- Thomas, Ernst (Hg.) (1965), Notation Neuer Musik (= Darmstädter Beiträge zur Neuen Musik, Bd. 9), Mainz: Schott.
- Vinci, Albert C. (1991), Die Notenschrift. Grundlagen der traditionellen Musiknotation , Kassel: Bärenreiter.
- Wanske, Helene (1988), Musiknotation. Von der Syntax des Notenstichs zum EDV-gesteuerten Notensatz, Maiz: Schott.
- Weizsäcker, Carl Friedrich von (1971), Die Einheit der Natur, München: Hanser.
- Wexelblat, Richard L. (Hg.) (1978), History of Programming Languages, New York: Academic Press. https://doi.org/10.1145/800025
- Wolf, Johannes (1917), Handbuch der Notationskunde, Wiesbaden: Breitkopf & Härtel.